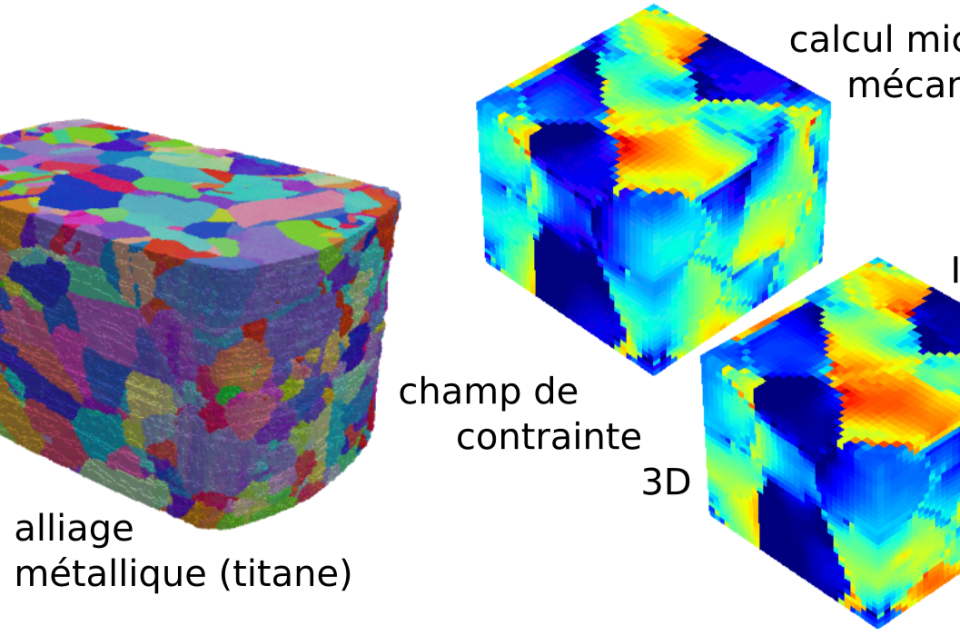
Optimisation stochastique : un important outil pour la prise de décision sous incertitude dans des problèmes industriels.
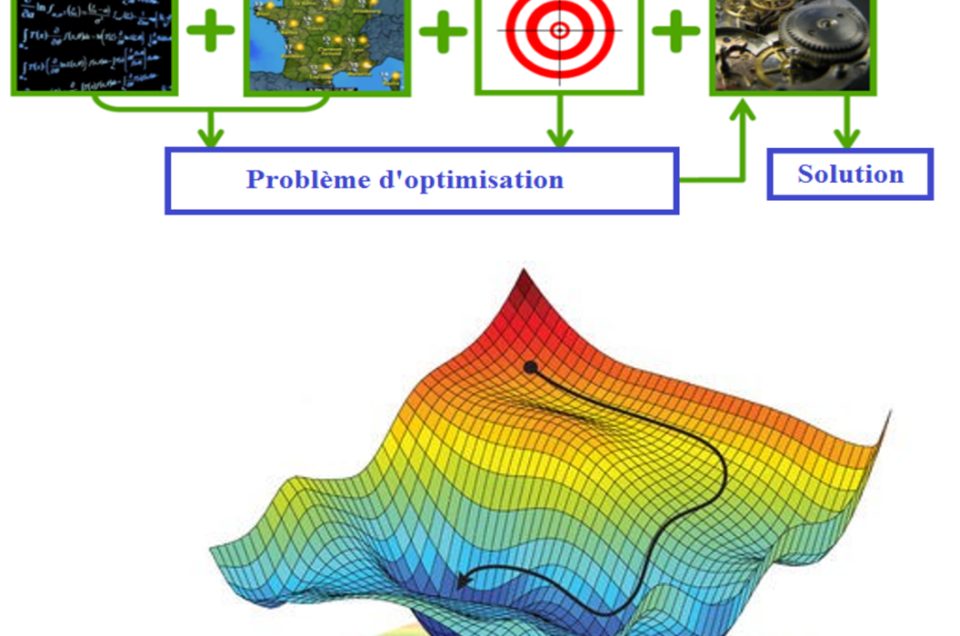
Les problèmes d’optimisation issus d’applications industriels sont souvent soumis à des données incertaines, telles que la demande, les prix, les ressources et les conditions météorologiques. En général, les données évoluent au fil du temps et les décisions doivent être prises à différentes étapes avant d’observer l’ensemble du flux de données. Au cœur des paradigmes de la prise de décision sous incertitude dans les problèmes industriels se trouve l’optimisation stochastique, une branche des mathématiques qui étudie la théorie et les méthodes pour résoudre des problèmes d’optimisation dépendant de paramètres aléatoires. En général, les modèles d’optimisation stochastique engendrent des problèmes d’optimisation de grande taille et/ou non convexes, qui ne peuvent être résolus qu’à l’aide d’algorithmes dédies.
Pour relever ces défis, le Centre de Mathématiques Appliquées de Mines Paris – PSL développe des méthodologies et des algorithmes avec garantie de converge, afin de rendre la prise de décision sous incertitudes plus systématique et efficace.
Contact : Welington De Oliveira
Centre : Le Centre de Mathématiques Appliquées (CMA)